=Start=
缘由:
想通过快速整理《机器学习实战》一书中出现过的各种机器学习算法的原理及其优缺点和适用范围来快速学习、了解常见的机器学习算法。
正文:
参考解答:
1、SVM简介
SVM的核心任务就是:构建一个N-1维的分割超平面来实现对N维样本数据放入划分,认定的分隔超平面两侧的样本点分属两个不同类别。
备注:超平面是纯粹的数学概念,不是物理概念,它是平面中的直线、空间中的平面的推广,只有当维度大于3时,才称为“超”平面。
对于SVM的另外一种理解:可以将线性不可分的数据,通过升维,进行线性可分。因为往往在低维空间下的非线性问题,转化到高维空间中,就变成了线性问题。
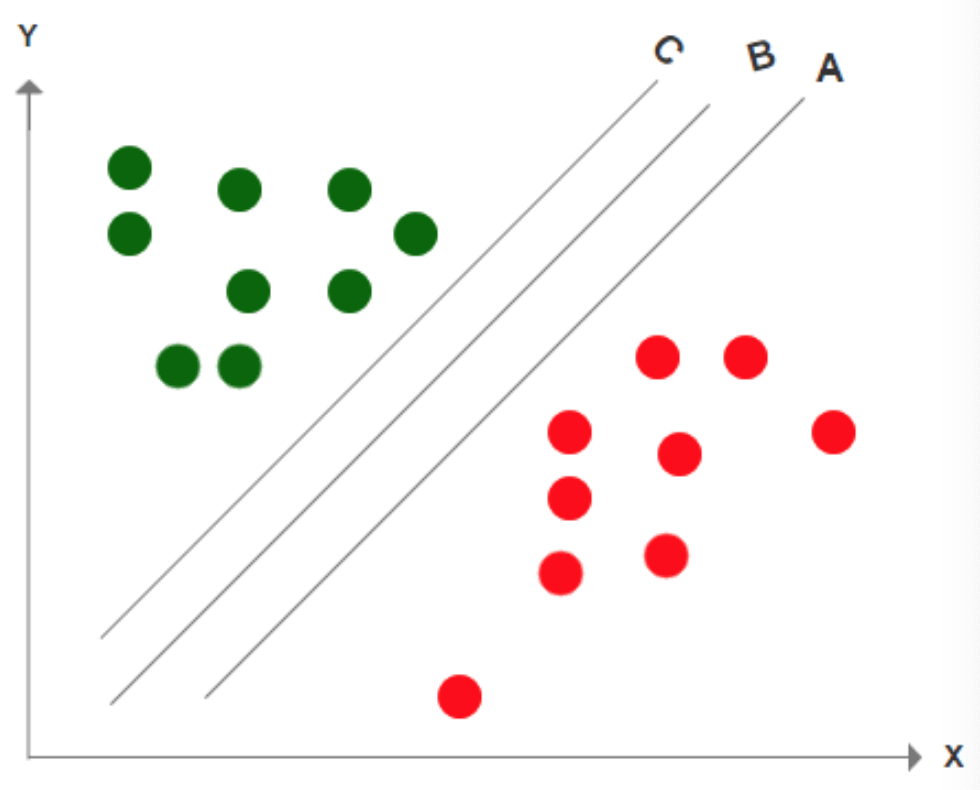
上图中,A、B、C三条线都完整的区分了边界,那我们应该如何选择呢?既然能分豆的工具这么多,那我们理所当然应该找一个最好的是不是?最佳答案应该是B,因为B与边数据的距离是最远的,之所以选择边距最远的线,是因为这样它的容错率更高,表现更稳定,也就是说当我们再次放入更多的豆的时候,出错的概率更小。
即,SVM的分类方法,首先考虑的是正确分类;其次考虑的优化数据到边界的距离。
2、核函数以及SVM的训练过程
核函数:任意两个样本点在扩维后的空间的内积,如果等于这两个样本点在原来空间经过一个函数后的输出,那么这个函数就叫核函数。
作用:有了这个核函数,以后的高维内积都可以转化为低维的函数运算了,这里也就是只需要计算低维的内积,然后再平方。明显问题得到解决且复杂度极大降低。总而言之,核函数它本质上隐含了从低维到高维的映射,从而避免直接计算高维的内积。
常用的核函数有如下一些:例如线性核函数、多项式核函数、径向基核函数(RBF)、高斯核函数、拉普拉斯核函数、sigmoid核函数等等。
简单的理解了SVM的原理,我们再来了解一下模型的训练过程。
- 被所有的样本和其对应的分类标记交给算法进行训练。
- 如果发现线性可分,那就直接找出超平面。
- 如果发现现行不可分,那就映射到n+1维的空间,找出超平面。
- 最后得到超平面的表达式,也就是分类函数。
3、SVM的优缺点
优点:
- 效果很好,分类边界清晰;
- 在高维空间中特别有效;
- 在空间维数大于样本数的情况下很有效;
- 它使用的是决策函数中的一个训练点子集(支持向量),所以占用内存小,效率高。
缺点:
- 如果数据量过大,或者训练时间过长,SVM会表现不佳;
- 如果数据集内有大量噪声,SVM效果不好;
- SVM不直接计算提供概率估计,所以我们要进行多次交叉验证,代价过高。
参考链接:
- SVM教程:支持向量机的直观理解#不错,易于理解
https://mp.weixin.qq.com/s/l1eqNOxf3Vb1SlPb-voPkA - 支持向量机(SVM)是什么意思?
https://www.zhihu.com/question/21094489 - 漫画:支持向量机 SVM
https://mp.weixin.qq.com/s/wNSerC7c_o0uHjgrNXLA1Q - AI产品经理必懂算法:支持向量机SVM#简洁明快
https://mp.weixin.qq.com/s/_vSr0CdnXYmwbZCYup4-Vg - 支持向量机SVM(一)
https://www.cnblogs.com/jerrylead/archive/2011/03/13/1982639.html - https://scikit-learn.org/stable/modules/svm.html
- https://en.wikipedia.org/wiki/Support_vector_machine
- http://bytesizebio.net/2014/02/05/support-vector-machines-explained-well/
=END=