=Start=
缘由:
了解常见算法的时间复杂度和空间复杂度对于一名程序员来说是大有裨益的——不论是准备考试、面试,还是方便自己学习、识记。
以往我在参加面试前,经常需要花费很多时间从互联网上查找各种搜索和排序算法的优劣,以便我在面试时不会被问住。也有针对性做了一些笔记,但时间一长,之前做的一些记录就都不知道放在哪去了,但现在我们可以通过 Eric 创建的 BigOCheatSheet 快速的了解常见算法的时空复杂度,省时省力,实乃居家旅行必备神器。
正文:
数据结构操作
| 数据结构 | 时间复杂度 | 空间复杂度 | |||||||
|---|---|---|---|---|---|---|---|---|---|
| 平均 | 最差 | 最差 | |||||||
| 访问 | 搜索 | 插入 | 删除 | 访问 | 搜索 | 插入 | 删除 | ||
| Array | O(1) | O(n) | O(n) | O(n) | O(1) | O(n) | O(n) | O(n) | O(n) |
| Stack | O(n) | O(n) | O(1) | O(1) | O(n) | O(n) | O(1) | O(1) | O(n) |
| Singly-Linked List | O(n) | O(n) | O(1) | O(1) | O(n) | O(n) | O(1) | O(1) | O(n) |
| Doubly-Linked List | O(n) | O(n) | O(1) | O(1) | O(n) | O(n) | O(1) | O(1) | O(n) |
| Skip List | O(log(n)) | O(log(n)) | O(log(n)) | O(log(n)) | O(n) | O(n) | O(n) | O(n) | O(n log(n)) |
| Hash Table | – | O(1) | O(1) | O(1) | – | O(n) | O(n) | O(n) | O(n) |
| Binary Search Tree | O(log(n)) | O(log(n)) | O(log(n)) | O(log(n)) | O(n) | O(n) | O(n) | O(n) | O(n) |
| Cartesian Tree | – | O(log(n)) | O(log(n)) | O(log(n)) | – | O(n) | O(n) | O(n) | O(n) |
| B-Tree | O(log(n)) | O(log(n)) | O(log(n)) | O(log(n)) | O(log(n)) | O(log(n)) | O(log(n)) | O(log(n)) | O(n) |
| Red-Black Tree | O(log(n)) | O(log(n)) | O(log(n)) | O(log(n)) | O(log(n)) | O(log(n)) | O(log(n)) | O(log(n)) | O(n) |
| Splay Tree | – | O(log(n)) | O(log(n)) | O(log(n)) | – | O(log(n)) | O(log(n)) | O(log(n)) | O(n) |
| AVL Tree | O(log(n)) | O(log(n)) | O(log(n)) | O(log(n)) | O(log(n)) | O(log(n)) | O(log(n)) | O(log(n)) | O(n) |
数组排序算法
| 算法 | 时间复杂度 | 空间复杂度 | ||
|---|---|---|---|---|
| 最佳 | 平均 | 最差 | 最差 | |
| Quicksort | O(n log(n)) | O(n log(n)) | O(n^2) | O(log(n)) |
| Mergesort | O(n log(n)) | O(n log(n)) | O(n log(n)) | O(n) |
| Timsort | O(n) | O(n log(n)) | O(n log(n)) | O(n) |
| Heapsort | O(n log(n)) | O(n log(n)) | O(n log(n)) | O(1) |
| Bubble Sort | O(n) | O(n^2) | O(n^2) | O(1) |
| Insertion Sort | O(n) | O(n^2) | O(n^2) | O(1) |
| Selection Sort | O(n^2) | O(n^2) | O(n^2) | O(1) |
| Shell Sort | O(n) | O((nlog(n))^2) | O((nlog(n))^2) | O(1) |
| Bucket Sort | O(n+k) | O(n+k) | O(n^2) | O(n) |
| Radix Sort | O(nk) | O(nk) | O(nk) | O(n+k) |
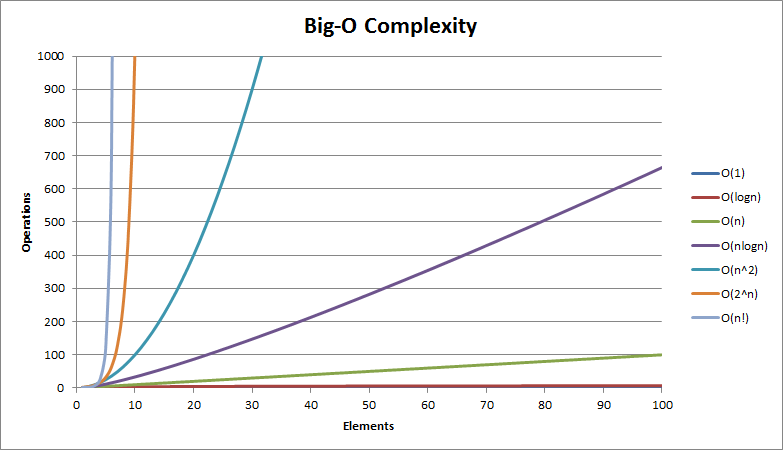
大O复杂度图表
参考链接:
- 原文链接:每个程序员都应该收藏的算法复杂度速查表
- 英文链接:http://bigocheatsheet.com/
- GitHub地址:BigOCheatSheet
=END=
《 “[collect]常见算法的时空复杂度备忘清单” 》 有 9 条评论
面试算法实践与国外大厂习题指南
https://zhuanlan.zhihu.com/p/25719965
https://github.com/kdn251/interviews/blob/master/README.md
https://github.com/kdn251/interviews/blob/master/README-zh-cn.md
算法实践,JS实现,排序,查找、树、两指针、动态规划等
https://github.com/qcer/Algo-Practice
算法数据结构中有哪些奇技淫巧?
https://www.zhihu.com/question/33776070
如何有效地写算法题
http://www.cnblogs.com/sskyy/p/8268976.html
`
目的
方法
分享
`
漏桶算法 && 令牌桶算法
http://int64.me/2018/%E6%BC%8F%E6%A1%B6%E7%AE%97%E6%B3%95%20&&%20%E4%BB%A4%E7%89%8C%E6%A1%B6%E7%AE%97%E6%B3%95.html
http://en.wikipedia.org/wiki/Token_bucket
http://en.wikipedia.org/wiki/Leaky_bucket
https://medium.com/smyte/rate-limiter-df3408325846
awesome算法文章索引
https://github.com/apachecn/awesome-algorithm/blob/master/README.md
如何在最短的时间内搞定数据结构和算法,应付面试?
https://www.zhihu.com/question/28580777
`
# 什么是数据结构?
简单说,数据结构就是一个容器,以某种特定的布局存储数据。这个“布局”使得数据结构在某些操作上非常高效,在另一些操作上则不那么高效。你的目标就是理解数据结构,这样就能为手头的问题选择最优的数据结构。
# 为什么我们需要数据结构?
由于数据结构用来以有组织的形式存储数据,而且数据是计算机科学中最重要的实体,因此数据结构的真正价值显而易见。
无论你解决什么问题,你都必须以这种或那种方式处理数据——员工的工资,股票价格,购物清单,甚至简单的电话簿等等。
根据不同的场景,数据需要以特定格式存储。目前有一些数据结构可以满足我们以不同格式存储数据的需求。
# 常用的数据结构
我们首先列出最常用的数据结构,然后再按个讲解:
数组
堆栈
队列
链表
树
图
字典树(Tries,这是一种高效的树,有必要单独列出来)
哈希表
`
数据结构和算法动态可视化 (Chinese)
https://visualgo.net/zh
16 年后重谈 P 和 NP
http://www.matrix67.com/blog/archives/7084
`
为什么 O(n2) 和 O(n · n!) 的差异那么大呢?原因就是,前者毕竟属于多项式级的增长,后者则已经超过了指数级的增长。
指数级的增长真的非常可怕,虽然 n 较小的时候看上去似乎很平常,但它很快就会超出你的想象,完全处于失控状态。一张纸对折一次会变成 2 层,再对折一次会变成 4 层……如此下去,每对折一次这个数目便会翻一倍。因此,一张纸对折了 n 次后,你就能得到 2n 层纸。当 n = 5 时,纸张层数 2n = 32;当 n = 10 时,纸张层数瞬间变成了 1024;当 n = 30 时,你面前将出现 230 = 1 073 741 824 层纸!一张纸的厚度大约是 0.1 毫米,这十亿多张纸叠加在一起,也就有 10 万多米。卡门线(Kármán line)位于海拔 100 千米处,是国际标准规定的外太空与地球大气层的界线。这表明,把一张纸对折 30 次以后,其总高度将会超出地球的大气层,直达外太空。
因而,在计算机算法领域,我们有一个最基本的假设:所有实用的、快速的、高效的算法,其时间复杂度都应该是多项式级别的。因此,在为计算机编写程序解决实际问题时,我们往往希望算法的时间复杂度是多项式级别的。这里的“问题”一词太过宽泛,可能会带来很多麻烦,因而我们规定,接下来所说的问题都是指的“判定性问题”(decision problem),即那些给定某些数据之后,要求回答“是”或者“否”的问题。
【在复杂度理论中,如果某个[判定性问题]可以用计算机[在多项式级别的时间内解出],我们就说这个问题是一个 P 问题,或者说它属于集合 P。这里,P 是“多项式”的英文单词 polynomial 的第一个字母。之前那个叠放东西的问题,就是一个 P 问题。】
对于有些问题来说,如果答案是肯定的,我们可能并没有一种非常明显的高效方法来检验这一点。不过,【很容易看出,找出一个多项式级的答案验核算法,再怎么也比找出一个多项式级的答案获取算法更容易。很多看上去非常困难的问题,都是先找到多项式级的答案验核算法,再找到多项式级的答案获取算法的。】一个经典的例子就是质数判定问题。如果某个数确实是一个质数,你怎样才能在多项式级的时间里证明这一点?1975 年,沃恩·普拉特(Vaughan Pratt)在《每个质数都有一份简短的证明书》(Every Prime Has a Succinct Certificate)一文中给出了一种这样的方法,无疑推动了质数判定算法的发展。
在复杂度理论中,一个问题有没有高效的答案验核算法,也是一个非常重要的研究课题。【对于一个判定性问题,如果存在一个多项式级的算法,使得每次遇到答案应为“是”的时候,我们都能向这个算法输入一段适当的“证据”,让算法运行完毕后就能确信答案确实为“是”,我们就说这个问题是一个 NP 问题,或者说它属于集合 NP。】为了解释“NP 问题”这个名字的来由,我们不得不提到 NP 问题的另一个等价定义:可以在具备随机功能的机器上用多项式级的时间解决的问题。
【所有的 P 问题一定都是 NP 问题,但反过来就不好说了。】例如,子集和问题是属于 NP 的。然而,之前我们就曾经讨论过,人们不但没有找到子集和问题的多项式级解法,而且也相信子集和问题恐怕根本就没有多项式级的解法。因而,子集和问题很可能属于这么一种类型的问题:它属于集合 NP,却不属于集合 P。
1971 年,史提芬·古克(Stephen Cook)发表了计算机科学领域最重要的论文之一——《定理证明过程的复杂性》(The Complexity of Theorem-Proving Procedures)。在这篇论文里,史提芬·古克提出了一个著名的问题:P 等于 NP 吗?如果非要用一句最简单、最直观的话来描述这个问题,那就是:【能高效地检验解的正确性,是否就意味着能高效地找出一个解?】数十年来,无数的学者向这个问题发起了无数次进攻。根据格哈德·韦金格(Gerhard Woeginger)的统计,仅从 1996 年算起,就有 100 余人声称解决了这个问题,其中 55 人声称 P 是等于 NP 的,另外 45 人声称 P 是不等于 NP 的,还有若干人声称这个问题理论上不可能被解决。但不出所料的是,所有这些“证明”都是错误的。目前为止,既没有人真正地证明了 P = NP,也没有人真正地证明了 P ≠ NP,也没有人真正地证明了这个问题的不可解性。这个问题毫无疑问地成为了计算机科学领域最大的未解之谜。在 2000 年美国克雷数学研究所(Clay Mathematics Institute)公布的千禧年七大数学难题(Millennium Prize Problems)中,P 和 NP 问题排在了第一位。第一个解决该问题的人将会获得一百万美元的奖金。
你或许会注意到,大家似乎都倾向于认为 P ≠ NP 。事实上,根据威廉·加萨奇(William Gasarch)的调查,超过八成的学者都认为 P ≠ NP。这至少有两个主要的原因。首先,证明 P = NP 看上去比证明 P ≠ NP 更容易,但即使这样,目前仍然没有任何迹象表明 P = NP。为了证明 P = NP,我们只需要构造一种可以适用于一切 NP 问题的超级万能的多项式级求解算法。在那篇划时代的论文里,史提芬·古克证明了一个颇有些出人意料的结论,让 P = NP 的构造性证明看起来更加唾手可得。给你一堆正整数,问能否把它们分成总和相等的两堆,这个问题叫作“分区问题”(partition problem)。容易看出,分区问题可以转化为子集和问题的一个特例,你只需要把子集和问题中的目标设定成所有数之和的一半即可。这说明,子集和问题是一个比分区问题更一般的“大问题”,它可以用来解决包括分区问题在内的很多“小问题”。史提芬·古克则证明了,在 NP 问题的集合里,存在至少一个最“大”的问题,它的表达能力如此之强,以至于一切 NP 问题都可以在多项式的时间里变成这个问题的一种特例。很容易想到,如果这样的“终极 NP 问题”有了多项式级的求解算法,所有的 NP 问题都将拥有多项式级的求解算法。这样的问题就叫作“NP 完全问题”(NP-complete problem)。在论文中,史提芬·古克构造出了一个具体的 NP 完全问题,它涉及到了很多计算机底层的逻辑运算,能蕴含所有的 NP 问题其实也不是非常奇怪的事。
P 等于 NP 吗?【能高效地检验解的正确性,是否就意味着能高效地找出一个解?】
虽然种种证据表明 P ≠ NP,但我们仍然无法排除 P = NP 的可能性。其实,如果 P 真的等于 NP,但时间复杂度的次数非常大非常大非常大,密码学的根基仍然不太可能动摇,我们的世界仍然不太可能大变。被誉为“算法分析之父”的计算机科学大师高德纳(Donald Knuth)还提出了这样一种可能:未来有人利用反证法证明了 P = NP,于是我们知道了所有 NP 问题都有多项式级的算法,但算法的时间复杂度究竟是多少,我们仍然一无所知!
我个人的简化版理解(不一定对):
P问题——可以用计算机在多项式级别的时间内【解出答案】的问题;
NP问题——可以有高效的(多项式级的)答案【验核】算法的问题;
NP完全问题——看上去像是一个 meta版本的 NP问题,它的表达能力很强,一般的NP问题可以认作是它的一个特例。
`