=Start=

缘由：

想通过快速整理《机器学习实战》一书中出现过的各种机器学习算法的原理及其优缺点和适用范围来快速学习、了解常见的机器学习算法。

正文：

参考解答：

1、逻辑回归简介

逻辑回归由统计学家 David Cox 于 1958 年提出。与传统的线性回归不同，逻辑回归（logistic regression）中响应变量（因变量）的取值不是连续的，而是离散的，每个取值代表一个不同的类别。因此，逻辑回归的本质是一个分类器（classifier）。它是一种有监督学习，通过训练集数据中的样本的特征向量 x 和标签 y（即响应变量的类别）来训练模型的参数，并使用该模型对未来的新样本进行分类。

最简单的逻辑回归中响应变量是二分类的（binary），即它仅仅可以取两个值，代表不同的两类。按照惯例，它的取值为 0 和 1。即便是最简单的模型也有广泛的应用，比如这两类可以代表着比赛中的输和赢、考试中的通过和失败、医疗领域的健康和生病、以及股市中的涨和跌等。如果响应变量的取值多于两类，则这样的问题叫做多项逻辑回归（multinomial logistic regression）。

在二元逻辑回归中，回归模型根据样本点的特征（features）计算该样本点属于每一类的条件概率。

关于逻辑回归，可以用一句话来总结：逻辑回归假设数据服从伯努利分布，通过极大似然函数的方法，运用梯度下降来求解参数，来达到将数据二分类的目的。

下文中如无特殊说明，当我们提到“逻辑回归”时，指代的都是最简单的二元逻辑回归。

2、sigmoid函数

首先我们了解一个函数：sigmoid，逻辑回归就是基于这个函数构建的模型。sigmod函数公式如下：

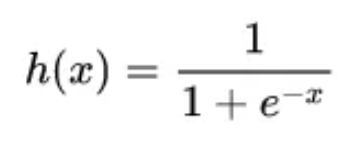
使用Python的numpy，matplotlib对该函数进行可视化，如下：

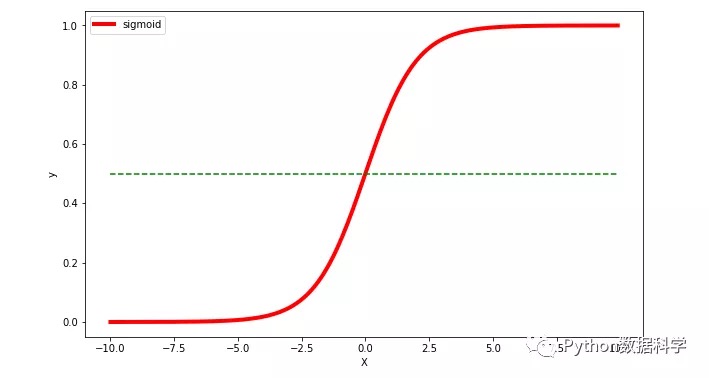
图中我们可以直观地看到这个函数的一些特点：

• 中间范围内函数斜率最大，对应Y的大部分数值变化
• Y轴数值范围在 0~1 之间
• X轴数值范围没有限制，但当X大于一定数值后，Y无限趋近于1，而小于一定数值后，Y无限趋近于0
• 特别地，当 X=0 时，Y=0.5

3、逻辑回归的优缺点

优点：

1. 直接对分类可能性进行建模，无需实现假设数据分布，这样就避免了假设分布不准确所带来的问题。
2. 形式简单，模型的可解释性非常好，特征的权重可以看到不同的特征对最后结果的影响。 
3. 除了类别，还能得到近似概率预测，这对许多需利用概率辅助决策的任务很有用。

缺点：

1. 准确率不是很高，因为形式非常的简单，很难去拟合数据的真实分布。
2. 本身无法筛选特征。

参考链接：

• 逻辑回归模型的前世今生
• 逻辑回归，很有逻辑#有例子易于理解
• 逻辑回归算法的原理及实现(LR)
• 逻辑回归：从入门到精通（全文20页下载）
• 机器学习：用初等数学解读逻辑回归
• 【机器学习笔记】：从零开始学会逻辑回归（一）
• 文科生都能看懂的机器学习教程：梯度下降、线性回归、逻辑回归
• https://scikit-learn.org/stable/modules/generated/sklearn.linear_model.LogisticRegression.html
• https://scikit-learn.org/stable/modules/generated/sklearn.linear_model.LogisticRegressionCV.html

=END=