=Start=
缘由:
简单整理一下期望、均值、方差、标准差、协方差的概念,方便在忘了的时候快速参考。
正文:
参考解答:
一维数据分析:
期望(Expectation)
概率论中描述一个随机事件中的随机变量的平均值的大小可以使用“数学期望”这个概念。数学期望的定义是实验中每次可能的结果的概率乘以其结果的总和。这又分为离散型和连续型随机变量的期望:
- 离散型
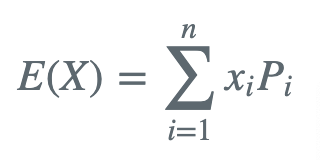
- 连续型
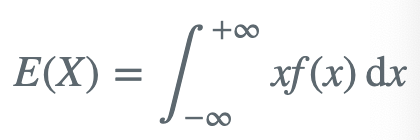
根据根据“大数定律”的描述,数学期望这个数字的意义是指随着重复次数接近无穷大时,数值的算术平均值几乎肯定收敛于数学期望值,也就是说数学期望值可以用于预测一个随机事件的平均预期情况。
均值(Mean)
![]()
均值的定义: 给定一个包含n个样本的集合 X={X1, …Xn},均值就是这个集合中所有元素和的平均值。
方差(Variance)
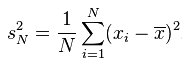
方差是在概率论和统计方差衡量随机变量或一组数据的离散程度的度量,换句话说如果想知道一组数据之间的分散程度的话就可以使用“方差”来表示了。
标准差(Standard Deviation)
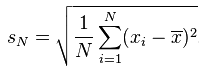
标准差又叫均方差,是”方差”的算术平方根,用 σ (sigma)表示。标准差能反映一个数据集的离散程度。平均数相同的两组数据,标准差未必相同。
标准差和方差一样都是用于衡量样本的离散程度的量,那么为什么要有标准差呢?因为方差和样本的“量纲”不一样,而标准差在量纲上与样本集合保持同步。这就是“标准”的意义了。
二维数据分析:
协方差(Covariance)
前面的方差/标准差描述的是一维数据集合的离散程度,但世界上的现象普遍是多维度数据描述的。那么很自然就会想知道现象和数据的相关程度,以及各维度数据间的相关程度。而协方差就是这样一种用来度量两个随机变量关系的统计量。
协方差的公式——期望值分别为 E(X) 和 E(Y) 的两个变量X和Y的协方差为:Cov(X,Y)=E[(X−E(X))(Y−E(Y))] 。
协方差可以通俗的理解为:两个变量在变化过程中是同方向变化?还是反方向变化?同向或反向程度如何?
- 你变大,同时我也变大,说明两个变量是同向变化的,这时协方差就是正的。
- 你变大,同时我变小,说明两个变量是反向变化的,这时协方差就是负的。
- 从数值来看,协方差的数值越大,两个变量同向程度也就越大。反之亦然。
相关系数(Correlation Coefficient)
对于相关系数,我们从它的公式入手。一般情况下,相关系数的公式为:
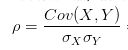
翻译一下:就是用X、Y的协方差除以X的标准差和Y的标准差。所以,相关系数也可以看成协方差:一种剔除了两个变量量纲影响、标准化后的特殊协方差。
既然是一种特殊的协方差,那它:
- 也可以反映两个变量变化时是同向还是反向,如果同向变化就为正,反向变化就为负。
- 由于它是标准化后的协方差,因此更重要的特性来了:它消除了两个变量变化幅度的影响,而只是单纯反应两个变量每单位变化时的相似程度。
参考链接:
- 标准差和方差
https://www.shuxuele.com/data/standard-deviation.html - 有了方差为什么需要标准差?
https://www.zhihu.com/question/20534502 - 数学期望、方差、标准差、协方差#nice
- 方差、标准差和协方差三者之间的定义与计算 #不错
https://www.cnblogs.com/xunziji/p/6772227.html - 一维数据分析:平均值(Mean)、方差(Variance)、标准差(Standard Deviation)
http://blog.shaochuancs.com/mean-variance-sd/ - 方差、标准差、均方差、均方误差区别总结
https://blog.csdn.net/Leyvi_Hsing/article/details/54022612 - 方差、标准差、均方差、均方误差
http://www.enkichen.com/2018/12/14/standard-deviation/ - 如何通俗易懂地解释「协方差」与「相关系数」的概念? #易懂
https://www.zhihu.com/question/20852004 - 协方差的意义和计算公式 #通俗易懂
https://www.cnblogs.com/ywl925/p/3210822.html - 如何通俗地理解协方差与相关系数?
https://www.matongxue.com/madocs/568/ - 期望、方差、协方差及相关系数的基本运算
https://blog.codinglabs.org/articles/basic-statistics-calculate.html - 通俗解释协方差与相关系数
https://redstonewill.com/1511/ - 关于协方差Covariance
https://www.hustyx.com/python/256/ - 方差和协方差
https://www.letiantian.me/2014-09-06-variance-and-covariance/ - 协方差(Covariance,COV)
- 方差var、协方差cov、协方差矩阵(浅谈)
- 协方差
=END=
《 “期望、方差、协方差及相关系数” 》 有 4 条评论
hive函数 — stddev , stddev_pop , stddev_samp , var_pop , var_samp
https://blog.csdn.net/lxpbs8851/article/details/39317611
`
当我们需要真实的标准差 方差的时候 最好是使用: stddev stddev_pop var_pop
而只是需要得到少量数据 标准差 方差 的近似值 可以选用: stddev_samp var_samp
`
Hive学习之内置聚合函数
https://blog.csdn.net/skywalker_only/article/details/38823387
`
stddev_pop(col)
返回组内某个数字列的标准差(DOUBLE类型)
stddev_samp(col)
返回组内某个数字列的无偏样本标准差(DOUBLE类型)
`
方差、标准差、均方差、均方误差(MSE)区别总结
https://zhuanlan.zhihu.com/p/83410946
`
那么问题来了,既然有了方差来描述变量与均值的偏离程度,那又搞出来个标准差干什么呢?
原因是方差与我们要处理的数据的量纲(单位)是不一致的,虽然能很好的描述数据与均值的偏离程度,但是处理结果是不符合我们的直观思维的。
举个例子:一个班级里有60个学生,平均成绩是70分,标准差是9,方差是81,假设成绩服从正态分布,那么我们通过方差不能直观的确定班级学生与均值到底偏离了多少分,通过标准差我们就很直观的得到学生成绩分布在[61,79]范围的概率为68%,即约等于下图中的34.2%*2
额外说明:一个标准差约为 68%(平均值-标准差,平均值+标准差), 两个标准差约为95%(平均值-2倍标准差,平均值+2倍标准差), 三个标准差约为99%。它反映组内个体间的离散程度。
从正态分布中抽出的一个样本落在[μ-3σ, μ+3σ]这个范围内的概率是99.7%,也可以称为“正负3个标准差”。
==
1、均方差就是标准差,标准差就是均方差
2、方差 是各数据偏离平均值 差值的平方和 的平均数
3、均方误差(MSE)是各数据偏离真实值 差值的平方和 的平均数
4、方差是平均值,均方误差是真实值。
总的来说,方差是数据序列与均值的关系,而均方误差是数据序列与真实值之间的关系,所以我们只需注意区分 真实值和均值 之间的关系就行了。
`
应用统计学:Z-score
https://mp.weixin.qq.com/s/Vg9Io680ivCaiy3iobQt5g
`
Z值(z-score,z-values, normal score)又称标准分数(standard score, standardized variable),是一个实测值与平均数的差再除以标准差的过程。Z score标准化是数据处理的一种常用方法。通过它能够将不同量级的数据转化为统一量度的Z score分值进行比较。
Z score通过(x-μ)/σ将两组或多组数据转化为无单位的Z score分值,使得数据标准统一化,提高了数据可比性,削弱了数据解释性。
Z-score的主要目的就是将不同量级的数据统一转化为同一个量级,统一用计算出的Z-score值衡量,以保证数据之间的可比性。Z值可以告诉我们整个数据相对于总体平均值的位置。Z 分数越高或越低,结果就越不可能偶然发生,结果就越有可能有意义。
Z-score最大的优点就是简单,容易计算,很多工具中,比如R,不需要加载包,仅仅凭借最简单的数学公式就能够计算出Z-score并进行比较。此外,Z-score能够应用于数值型的数据,并且不受数据量级的影响,因为它本身的作用就是消除量级给分析带来的不便。
但是Z-score应用也有风险。首先,估算Z-score需要总体的平均值与方差,但是这一值在真实的分析与挖掘中很难得到,大多数情况下是用样本的均值与标准差替代。其次,Z-score对于数据的分布有一定的要求,正态分布是最有利于Z-score计算的。最后,Z-score消除了数据具有的实际意义,A的Z-score与B的Z-score与他们各自的分数不再有关系,因此Z-score的结果只能用于比较数据间的结果,数据的真实意义还需要还原原值。
`
68–95–99.7法则
https://zh.wikipedia.org/wiki/68%E2%80%9395%E2%80%9399.7%E6%B3%95%E5%89%87
`
在统计上,68–95–99.7法则(68–95–99.7 rule)是在正态分布中,距平均值小于一个标准差、二个标准差、三个标准差以内的百分比,更精确的数字是68.27%、95.45%及99.73%。
在实验科学中有对应正态分布的三西格马法则(three-sigma rule of thumb),是一个简单的推论,内容是**“几乎所有”的值都在平均值正负三个标准差的范围内,也就是在实验上可以将99.7%的概率视为“几乎一定”**。不过上述推论是否有效,会视探讨领域中“显著”的定义而定,在不同领域,“显著”(significant)的定义也随着不同,例如在社会科学中,若置信区间是在正负二个标准差(95%)的范围,即可视为显著。但是在粒子物理中,若是发现新的粒子,置信区间要到正负五个标准差(99.99994%)的程度。
在不是正态分布的情形下,也有另一个对应的三西格马法则(three-sigma rule),**即使是在非正态分布的情形下,至少会有88.8%的概率会在正负三个标准差的范围内,这是依照切比雪夫不等式的结果**。若是单模分布(unimodal distributions)下,正负三个标准差内的概率至少有95%,若一些符合特定条件的分布,概率至少会到98%。
`
正态分布
https://zh.wikipedia.org/wiki/%E6%AD%A3%E6%80%81%E5%88%86%E5%B8%83
`
正态分布(Normal distribution),又名高斯分布(英语:Gaussian distribution)、正规分布,是一个非常常见的连续概率分布。正态分布在统计学上十分重要,经常用在自然和社会科学来代表一个不明的随机变量。
正态分布是自然科学与行为科学中的定量现象的一个方便模型。各种各样的心理学测试分数和物理现象比如光子计数都被发现近似地服从正态分布。尽管这些现象的根本原因经常是未知的,理论上可以证明如果把许多小作用加起来看做一个变量,那么这个变量服从正态分布(在R.N.Bracewell的Fourier transform and its application中可以找到一种简单的证明)。正态分布出现在许多区域统计:例如,采样分布均值是近似地正态的,即使被采样的样本的原始群体分布并不服从正态分布。另外,正态分布信息熵在所有的已知均值及方差的分布中最大,这使得它作为一种均值以及方差已知的分布的自然选择。正态分布是在统计以及许多统计测试中最广泛应用的一类分布。在概率论,正态分布是几种连续以及离散分布的极限分布。
==
question:
如何判断数据是否服从正态分布?有没有什么简单好用的判断方法?网站的Nginx访问日志数据服从正态分布吗?为什么?
answer:
要判断数据是否服从正态分布,可以使用以下方法:
1. 直方图:绘制数据的直方图并观察其形状。正态分布的直方图通常呈现出钟形曲线,对称分布,并且均值、中位数和众数相等。
2. Q-Q 图:绘制数据的 Q-Q 图(Quantile-Quantile Plot)。Q-Q 图将数据的分位数与正态分布的分位数进行比较。如果数据点近似沿着一条直线分布,那么数据可能服从正态分布。
3. Shapiro-Wilk 正态性检验:这是一种常用的统计检验方法,用于检验数据是否来自正态分布。该检验的零假设是数据来自正态分布。如果 p 值小于显著性水平(通常为 0.05),则可以拒绝零假设,即数据不服从正态分布。
关于 Nginx 访问日志数据是否服从正态分布,需要考虑以下几点:
1. 数据类型:Nginx 访问日志通常包含访问时间、IP 地址、请求路径等信息,这些数据通常是离散的或者具有特定的分布模式,并不是连续的数值型数据。因此,对于这种类型的数据,正态分布并不是一个合适的假设。
2. 数据量和采样方式:如果你有足够大的数据集并且是随机采样的,可以进行上述的正态性检验。但是请注意,即使数据服从正态分布,也可能存在一些离群值或异常值。
3. 领域知识:更重要的是,对于特定的数据集和应用场景,你应该考虑领域知识。了解数据的生成方式、特点以及可能的分布模式,会对判断数据是否服从正态分布提供更有意义的线索。
综上所述,对于 Nginx 访问日志数据,正态分布通常不是一个适用的假设。你可以使用适合该数据类型的其他分布或模型进行分析和建模。
`